- 第一讲
- 第二讲
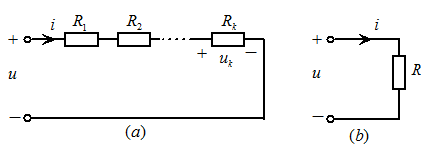
图2.1电阻串联及其等效电路
如图2.1 电路所示,多个电阻顺序相连,流过同一电流的连接方式,称之为电阻串联。电阻串联时电路具有以下特点:
电路所示,多个电阻顺序相连,流过同一电流的连接方式,称之为电阻串联。电阻串联时电路具有以下特点:
(1)所有电阻流过同一电流。
(2)由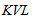 可知,
可知,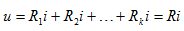 ,其中
,其中
 (2.1)
(2.1)
称之为电阻串联的等效电阻,它等于所有串联电阻之和。其等效电路如图2.1 所示。
所示。
(3)所有电阻消耗的总功率:
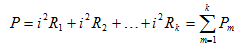 (2.2)
(2.2)
即所有电阻消耗的总功率等于各个电阻消耗的功率之和。
(4)电阻分压公式:
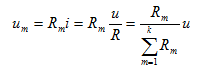 (2.3)
(2.3)

图2.2电阻并联及其等效电路
如图2.2 电路所示,多个电阻首端相连、末端相连,施加同一电压的连接方式,称之为电阻并联。电阻并联时电路具有以下特点:
电路所示,多个电阻首端相连、末端相连,施加同一电压的连接方式,称之为电阻并联。电阻并联时电路具有以下特点:
(1)所有电阻施加同一电压。
(2)由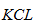 可知,
可知,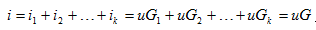 ,其中
,其中
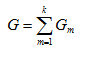 (2.4)
(2.4)
称之为电阻并联的等效电导,它等于所有并联的电导之和。其等效电路如图2.2 所示。
所示。
(3)所有电阻消耗的总功率:
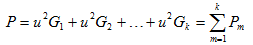 (2.5)
(2.5)
即所有电阻消耗的总功率等于各个电阻消耗的功率之和。
(4)电阻分流公式:
 (2.6)
(2.6)
多个电阻部分串联、部分并联的联接方式称为混联。混联时应该用电阻的串、并联特点逐步化简。
例2.1如图2.3 所示电路,求其等效电路。
所示电路,求其等效电路。
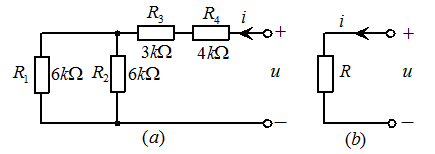
图2.3
解:图2.3中电阻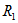 和
和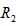 是并联,
是并联,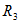 和
和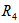 是串联,然后两者再串联。则
是串联,然后两者再串联。则

其等效电阻
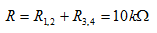
其等效电路如图2.3 所示。
所示。
四.电阻的Y型及△联接及其等效变换
具有三个引出端且内部无任何电源(独立源与受控源)的电路,称为无源三端电路。图2.4即为两个无源三端电路,其中图 称为Y型联接(也称星型联接或T型联接);图
称为Y型联接(也称星型联接或T型联接);图 称为
称为 联接(也称三角形联接或,用
联接(也称三角形联接或,用 型联接)。
型联接)。
在电路分析中可把这两种无源三端电路进行相互等效变换,其等效变换的条件是对应节点上的端电流相等,即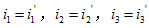 ;相应两节点的电压相等,即
;相应两节点的电压相等,即
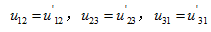
下面推到它们两者相互等效交换的公式。

图2.4无源三端电路
对于图2.4 电路有
电路有
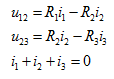 (2.7)
(2.7)
对式(2.7)求解,得
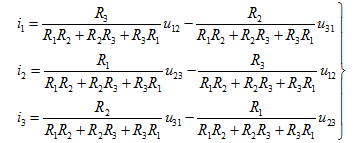 (2.8)
(2.8)
对于图2.4 电路有
电路有
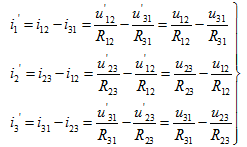 (2.9)
(2.9)
根据等效变换,应有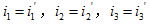 ,故式(2.8)和式(2.9)应相等,且对应项的系数也应相等。于是得
,故式(2.8)和式(2.9)应相等,且对应项的系数也应相等。于是得
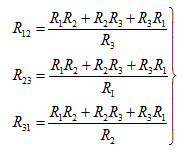 (2.10)
(2.10)
式(2.10)即为由已知的星形联接求等效三角形联接的公式。
当 时,则有
时,则有
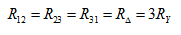 (2.11)
(2.11)
由式(2.10)可解得
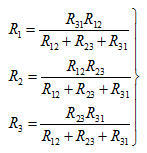 (2.12)
(2.12)
式(2.12)即为由已知的三角形联接求等效星形联接的公式。
当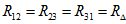 时,则有
时,则有
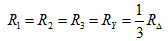 (2.13)
(2.13)
例2.2求图2.5所示电路的等效电阻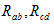 。
。

(1) (2)
图2.5
解:通过同一电流的元件为串联;两端为同一电压的元件为并联;无电流通过的元件可开路;电位相同的节点可短路。因此
(1)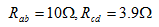
(2)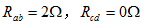
例2.3求图2.6 所示电路的等效电阻
所示电路的等效电阻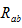 。
。
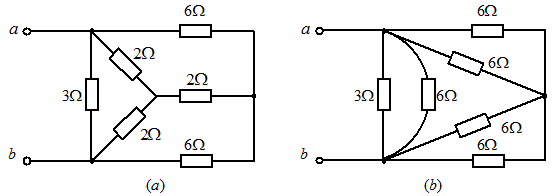
图2.6
解:在图2.6 所示电路中,很显然三个
所示电路中,很显然三个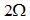 的电阻是Y型联接的,可将其转换成△联接,如图2.6
的电阻是Y型联接的,可将其转换成△联接,如图2.6 所示。则
所示。则