一．理想电源的联接及其等效变换

如图2.7所示电路，为理想电压源的串联，即所连接的各电压源流过同一电流。由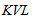可知，可等效为一个理想电压源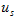，其等效电路如图2.7所示。

一般情况，理想电压源不允许并联。只有电压数值、极性完全相同的理想电压源才可并联。

图2.7理想电压源串联及其等效电路　　　　　　　　图2.8理想电流源并联及其等效电路

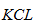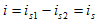如图2.8所示电路，为理想电流源的并联，即所连接的各电流源端均为同一电压。由可知，可等效为一个理想电流源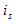，其等效电路如图2.8所示。

一般情况，理想电流源不允许串联。只有电流数值、方向完全相同的理想电流源才可串联。

二．实际电压源模型及其伏安关系

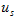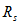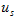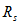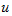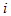一个实际的电源可用一个理想电压源和一个电阻的串联组合来作为其电路模型，如图2.9所示，称为电压源模型。其中为电压源的电压，为它的内电阻（也称电压源的输出电阻），和分别为其端电压和端电流。

图2.9电压源模型及其伏安特性

根据图2.9可写出电压源模型的伏安方程为

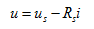　　　（2.14）

输出电流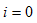时称为电压源端口开路，如图2.9所示。端口开路时的端电压称为开路电压，用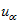表示。

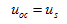
端电压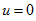时称为电压源端口短路，如图2.9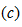所示。端口短路时的电流称为短路电流，用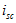表示。由式（2.14）可见有

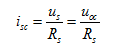　　　（2.15）

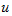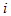与的关系曲线如图2.9(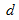)所示。此曲线称为电压源的伏安特性，也称外特性。可见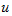随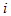的增大而线性减小。

三．实际电流源模型及其伏安关系

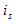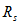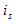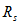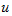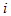一个实际电源也可用一个理想电流源和一个电阻的并联组合来作为其电路模型。如图2.10所示，称为电流源模型。其中为电流源的电流，为它的内电阻（也称电流源的输出电阻），和分别为其端电压和端电流，箭头表示电流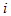的参考方向。

根据图2.10可写出电流源模型的伏安方程为

　　　（2.16）

端电压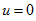时称为电流源端口短路，如图2.10所示。短路电流为

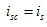
输出电流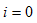时称为电流源端口开路，如图2.10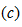所示。开路电压为

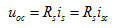　　　（2.17）

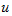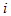与的关系曲线如图2.10(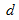)所示。此曲线称为电流源的伏安特性，也称外特性。可见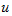随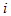的增大也是线性减小。

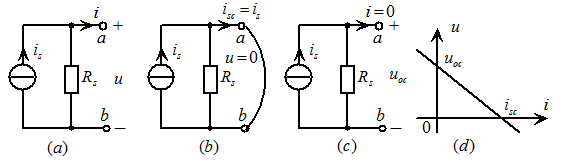
图2.10电流源模型及其伏安特性

四．实际电源模型的等效变换

为了电路分析的需要，我们往往将电压源模型和电流源模型进行相互变换，当这种相互变换是在保持两者外特性（即伏安关系曲线）完全相同的原则下进行时，即为等效变换。

1.电压源模型等效变换为电流源模型

电压源如图2.11所示。根据其伏安关系，有

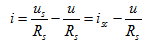　　　（2.18）

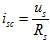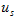其中为电压源模型的端口短路电流。根据式（2.18）即可画出与之对应的等效电路，如图2.11所示，称为电压源模型的等效电流源模型。可将这种等效变换原则总结为三条：①与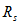的串联组合变为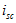与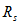的并联组合；②等效电流源模型的电流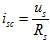，为电压源模型的端口短路电流；③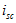的方向与电压源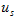的从“-”指向“+”的方向一致。

2.电流源模型等效变换为电压源模型

电流源模型如图2.12所示。根据其伏安关系，有

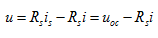　　　（2.19）

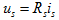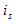其中为电流源模型的端口开路电压。根据式（2.19）即可画出与之对应的等效电路，如图2.12所示，称为电流源模型的等效电压源模型。可将这种等效变换原则总结为三条：①与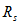的并联组合变为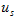与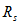的串联组合；②等效电压源模型的电压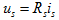，为电流源模型的端口开路电压；③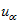的极性为从“—”到“+”与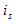的方向一致。

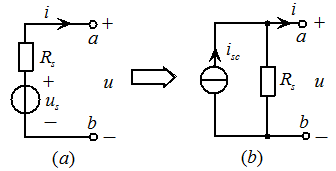
图2.11电压源模型等效变换为电流源模型

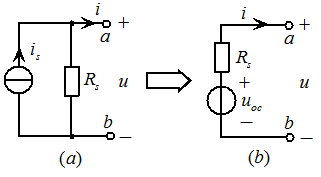
图2.12电流源模型等效变换为电压源模型

几点说明：

⑴电源模型的等效变换只是对外部电路等效，对电源模型内部是不等效的；

⑵实际电源在进行电源的等效变换时注意等效参数的计算、电源数值与方向的关系。

⑶理想电压源与理想电流源不能互相等效变换，即理想电压源不存在与之对应的等效电流源，理想电流源也不存在与之对应的等效电压源。

⑷受控电压源与受控电流源相互等效变换的原则与上述原则全同。

⑸与理想电压源并联的支路对外可以开路等效；与理想电流源串联的支路对外可以短路等效。

例2.4求图2.13所示电路化简为最简等效电路。

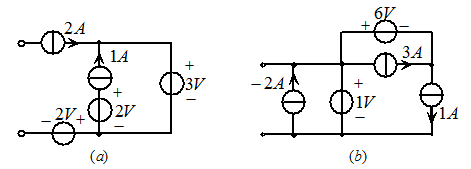
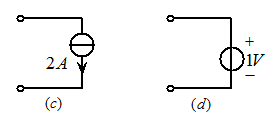
图2.13

解：利用理想电源的基本性质和等效变换的意义。

图2.13可等效变换为一个理想的电流源，如下图()所示。图2.13可等效变换为一个理想的电压源，如下图(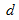)所示。

1. 求图2.14所示电路中的电流。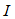

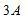解：由图2.14可知，先将与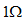并联的实际电流源转化为电压源，将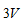与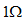串联的实际电压源转化为电流源，如图2.14所示。在图2.14中，将两个理想电流源合并，再将其实际电流源转化为电压源，如图2.14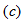所示。

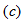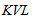在图2.14中，应用有：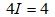

故

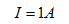
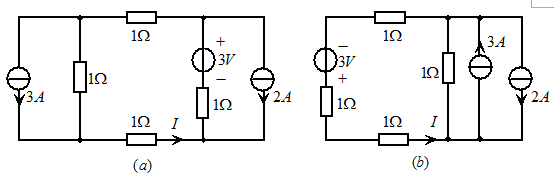
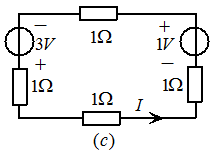
图2.14