- 第一讲
- 第二讲
图4.1(a)所示的电路,现在用网孔法求电流 ,其网孔方程为
,其网孔方程为
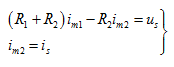
联解得
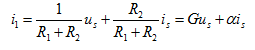 (4.1)
(4.1)
其中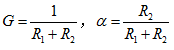 ,为两个比例常数,其值完全由电路的结构与参数决定。
,为两个比例常数,其值完全由电路的结构与参数决定。
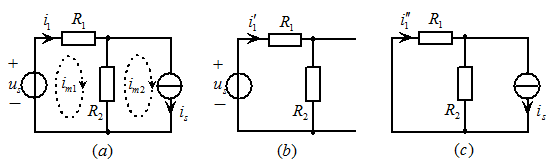
图4.1叠加定理
由式(4.1)可见,响应电流 为激励
为激励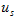 与
与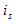 的线性组合函数,它由两个分量组成。一个分量
的线性组合函数,它由两个分量组成。一个分量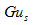 只与
只与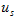 有关,另一个分量
有关,另一个分量 只与
只与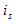 有关。
有关。
当 (就是将电流源
(就是将电流源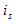 开路)时,电路中只有
开路)时,电路中只有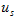 单独作用,如图4.1(b)所示。此时得
单独作用,如图4.1(b)所示。此时得
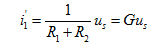
当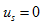 (就是将电压源
(就是将电压源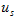 短路)时,电路中只有
短路)时,电路中只有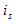 单独作用,如图4.1(c)所示。此时得
单独作用,如图4.1(c)所示。此时得
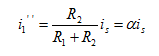
由以上三式得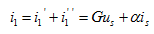
此结果说明,两个独立电源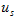 与
与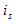 同时作用在电路中产生的响应
同时作用在电路中产生的响应 ,等于每个独立电源单独作用时在电路中所产生响应
,等于每个独立电源单独作用时在电路中所产生响应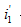 与
与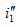 的代数和。将此结论推广即得叠加定理。
的代数和。将此结论推广即得叠加定理。
叠加定理的内容:线性电路中所有独立电源同时作用时在每一条支路中所产生的响应电流或电压,等于各个独立电源单独作用时在该支路中所产生响应电流或电压的代数和。叠加定理也称叠加性。
叠加定理反映了线性电路中各独立电源的独立性。
几点说明:
(1)叠加定理只能适用于线性电路,不适用于非线性电路;
(2)一个独立电源单独作用时,其余独立电源为零,即理想电压源短路,理想电流源开路;
(3)任一独立电源单独作用时,受控源均要保留,且其控制关系不变;
(4)一个独立电源单独作用时,其余独立电源为零,而电路的其余结构都不改变;
(5)叠加的结果为代数和,因此注意电压或电流的参考方向;
(6)叠加定理不能用于计算功率,这是因为功率不是电压或电流的一次函数。
例4.1图4.2电路,已知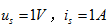 时,
时,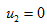 ;当
;当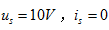 时,
时,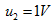 。求
。求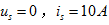 时的
时的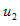 值。
值。
解:根据叠加定理,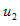 应是
应是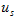 和
和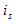 的线性组合函数,即
的线性组合函数,即
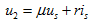 (4.2)
(4.2)
其中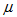 和r为比例常数。
和r为比例常数。
将已知数据代入(4.2)可求得: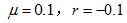 。
。
因此,有
 (4.3)
(4.3)
当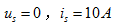 时,即
时,即
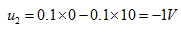

图4.2
- 用叠加定理求图4.3
 电路中的u,i。
电路中的u,i。

图4.3
解:
用叠加定理分析含受控源电路,当某一独立源单独作用时,其余的独立源均应为零,但所有受控源均应保留,因为受控源不是激励,且具有电阻性。
10V独立电压源单独作用时的电路如图4.3 所示,可求得
所示,可求得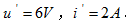 ,
,
3A独立电流源单独作用时的电路如图4.3 所示,可求得
所示,可求得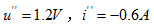 。故得
。故得
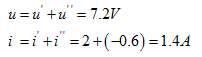
给式(4.1)等号两端同乘以常数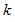 ,即有
,即有
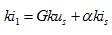
此结果正是齐次定理所表述的内容,即:在线性电路中,当全部激励(独立电压源和独立电流源)同时增大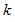 (
(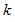 为实常数)倍时,其响应也相应增大
为实常数)倍时,其响应也相应增大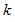 倍。此结论称为齐次定理,也称齐次性。
倍。此结论称为齐次定理,也称齐次性。
齐次定理反映了线性电路中激励与响应的比例关系。
几点说明:
(1)齐次定理只能适用于线性电路,不适用于非线性电路;
(2)激励是指独立电源;响应是指电压或电流;
(3)只有全部激励同时增大或缩小K倍时,响应才同时增大或缩小K倍。否则将导致错误的结果;
(4)齐次定理不能用于功率计算;
(5)当电路只有一个激励时,响应将与激励成正比。
同时满足其次性与叠加性的电路称为线性电路。齐次性与叠加性是线性电路极重要的性质。
需要指出的是,齐次定理与叠加定理是线性电路两个互相独立的性质,不能用叠加定理代替齐次定理,也不能片面认为齐次定理是叠加定理的特例。