在线性无任何电源（独立源与受控源）的传输网络中，当网络的激励与响应的位置互换

时，同一的激励奖产生相同的响应。此结论称为互易定理，也称互易性。它说明了线性无源网络传输信号的双向性或可逆性，即从甲方向乙方传输的效果，从乙方向甲方传输的效果全同。

互易定理的内容有三。

在图4.15所示的线性无任何电源的电阻网络P中，设加在输入端口1、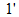的为电

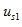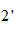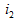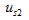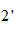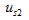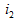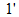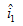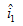压激励，在输出端口2、短路导线中产生的响应电流为；今把电压激励加在端口2、，如图4.15所示（注意的极性与的方向的关系），在端口1、短路导线中产生的响应电流为（注意的方向与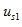的极性的关系），则有

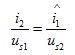　　　　（4.9）

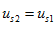当取时，则有

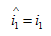　　　（4.10）

式（4.9）和式（4.10）的意义即为互易定理一。

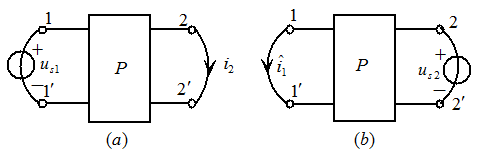
图4.15互易定理一

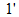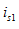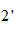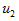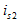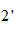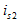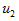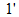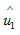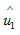如图4.16所示，设加在1、端口的为电流激励，而在2、端口的响应为开路电压；今把电流激励加在2、端口，如图4.16所示（注意的方向与的极性的关系），在1、端口的响应为开路电压（注意的极性与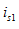的方向的关系），则有

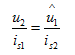　　　（4.11）

当取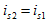时，则有

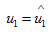　　　（4.12）

式（4.11）和式（4.12）的意义即为互易定理二。

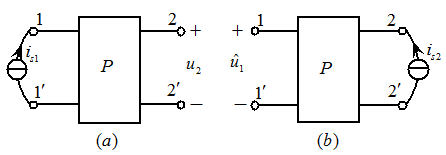
图4.16互易定理二

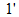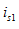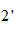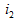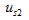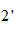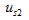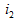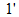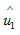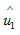如图4.17所示，设加在1、端口的为电流激励，而在2，端口的短路电流为；把电压激励加在2、端口，如图4.17所示（注意的极性与的方向的关系），在1、端口的开路电压为（注意的极性与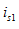的方向的关系），则有

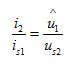　　　（4.13）

当在数值上取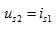时，则在数值上就有

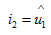　　　（4.14）

式（4.13）和式（4.14）的意义即为互易定理三。

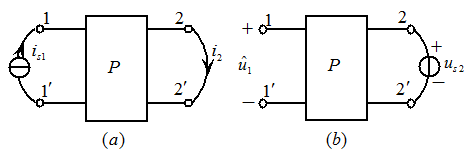
图4.17互易定理三

互易性是线性无源网络的一个重要性质，在分析网络的传输特性以及接收天线的方向性等方面要经常用到，在电路的计算方面也有用处。

满足互易性的网络称为互易网络。

互易定理说明了线性不含任何电源的电路中传输信号的双向性或可逆性。

几点说明

（1）互易定理只是用于线性电路，不适用于非线性电路；

（2）互易定理所述的激励是指电压源或电流源；响应是指电流或电压；

（3）只有激励与响应互换位置，电路其余结构均不能发生变化；

（4）在互易定理形式1和形式2中，激励与响应不能同时为同一量纲；在形式3种，虽然激励与响应同时为同一量纲，但互易前后两网络的激励与响应满足对偶关系。

例4.9图4.18中的数据已知，求图4.18中的电流。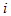

解：

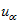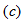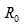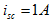将图4.18a,b端以右的电路用一个等效电压源替代，如图4.18(e)所示，等效电压源的电压，按图4.18求之为5V（根据互易定理二）。为求得等效电压源的内阻，可根据互易定理三，按图4.18求得，于是得

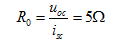
故据图4.18(e)得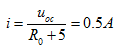　　　　　　　　　　　　　　　

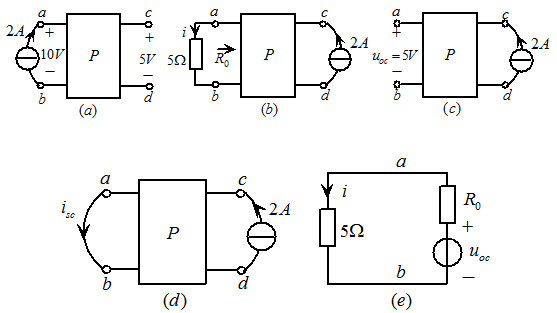
图4.18

1. 图4.19为一互易网络，已知中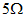电阻吸收的功率为125W，求。

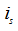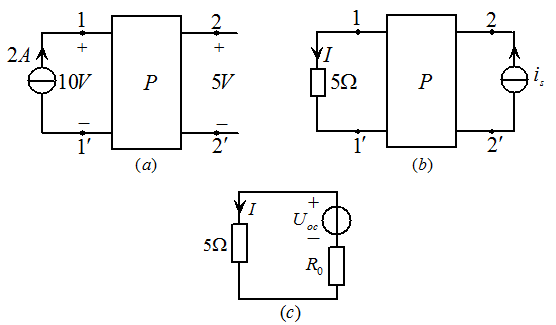
图4.19

解：

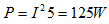由图4.19可知：，所以：。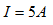

从图4.19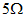电阻两端看进去的戴维南等效电路如图4.19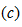所示：

由图4.19可知：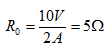

所以：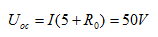　　　　　　　　　　　　　　　　

由互易定理2可知：

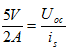，即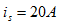。