- 第一讲
- 第二讲
正弦量在时域常用两种方式表示。一种是以波形的形式表示,如图5.4所示,其中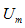 ,
,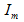 分别为正弦量
分别为正弦量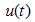 ,
,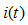 的最大值;T为周期,即正弦量变化一个循环所经历的时间,单位为秒
的最大值;T为周期,即正弦量变化一个循环所经历的时间,单位为秒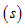 。正弦量每秒变化的循环个数称为频率,用
。正弦量每秒变化的循环个数称为频率,用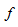 表示,单位为赫兹
表示,单位为赫兹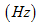 。显然有
。显然有
 (5.1)
(5.1)
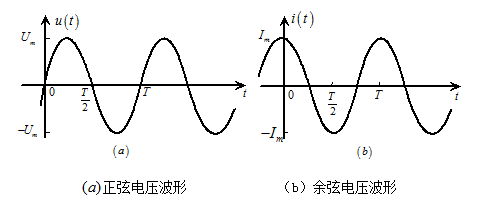
图5.4正弦量波形表示
正弦量时域的另一种表示是用正弦函数表达式或与余弦函数表达式。本书采用余弦函数表达式,但仍称为正弦函数或正弦量。例如正弦电压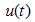 、正弦电流
、正弦电流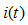 可分别表示为
可分别表示为
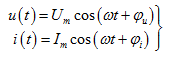 (5.2)
(5.2)
式中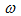 称为角频率,它表征正弦量变化的快慢,单位为弧度/秒
称为角频率,它表征正弦量变化的快慢,单位为弧度/秒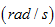 ,且有
,且有
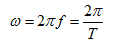 (5.3)
(5.3)
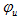 和
和 分别表示
分别表示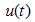 和
和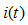 的初相位。
的初相位。
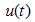 和
和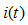 表示了正弦量在任一时刻的值,称为瞬时值。瞬时值均用小写字母表示,如
表示了正弦量在任一时刻的值,称为瞬时值。瞬时值均用小写字母表示,如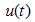 ,
,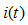 ,有时为了简便,也直接写成
,有时为了简便,也直接写成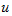 ,
,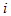 ,不言而喻,这均指随时间t变化的瞬时表示。
,不言而喻,这均指随时间t变化的瞬时表示。
可见,可以用最大值、角频率(或频率、周期)和初相位来描述一个正弦量的瞬时值随时间变化的全貌,因此,将这三个量称为正弦量的三要素。
二.正弦量的相位差设有两个同频率的正弦量,例如一个是电压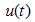 ,一个是电流,
,一个是电流,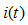 如式(5.2)所示,则定义它们两者的相位差为
如式(5.2)所示,则定义它们两者的相位差为
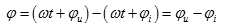 (5.4)
(5.4)
可见两个同频率的正弦量的相位差等于它们初相位之差,且为一常数,与时间变量t无关。 采用主值范围内的度或弧度为单位。
采用主值范围内的度或弧度为单位。
为了比较同频率的各个正弦量之间的相互关系,通常可任意选择其中一个正弦量,令其初相位为零,此正弦量称为参考正弦量。一旦选定参考正弦量,则其余正弦量的相位关系都以参考正弦量为准,具有一定的初相位。在同一电路中,参考正弦量的选择是任意的,但只能选一个。
相位差的物理意义是表示两个同频率正弦量随时间变化“步调”上的先后,当相位差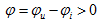 时,则称
时,则称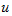 在相位上超前于
在相位上超前于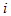 ,或
,或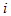 滞后于
滞后于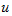 一个角度
一个角度 ;若
;若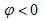 ,则
,则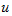 滞后
滞后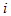 一个角度
一个角度 ,或
,或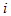 超前于
超前于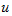 一个角度
一个角度 ;若
;若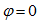 ,则称
,则称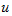 与
与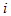 同相位;若
同相位;若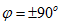 ,则称
,则称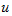 与
与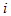 在相位上相互正交;若
在相位上相互正交;若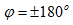 ,则称
,则称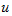 与
与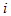 反相位。
反相位。
应当指出,只有同频率的正弦量在任意时刻的相位差是恒定的,而不同频率正弦量的相位差是随时间变化的,因而是没有意义的。
例5.2已知两个同频率的正弦电压
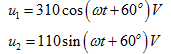
求两个正弦量的相位差 并说明其相位关系。
并说明其相位关系。
解欲求两个同频率正弦量的相位差,必须将它们用同一种函数表示,故将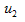 写为
写为

即 ,故得
,故得
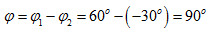
这表明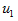 超前于
超前于 ,或这
,或这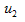 滞后于
滞后于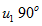 ,并且
,并且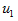 和
和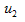 是正交的。
是正交的。
由于正弦量是时间变量的函数,其瞬时值时随时间变化的,所以不论是测量还是计算都不方便。为此对于此类随时间按周期变化的量需引入有效值的物理量。有效值用大写字母表示。
设电流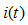 是一个周期变化的电流,则其有效值定义为
是一个周期变化的电流,则其有效值定义为
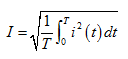 (5.5)
(5.5)
即有效值等于周期电流在一个周期内的方均根值。它的物理意义是指在同一电阻R中先后通以直流电流I和周期电流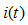 ,若在周期电流的一个周期T时间内,两者产生的热量相等,即
,若在周期电流的一个周期T时间内,两者产生的热量相等,即
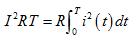
则得式(5.5)。换言之,周期电流的有效值是与它热效应相等的直流电流的值。说明:
(1)有效值需用大写字母表示,且有效值恒大于等于零。
(2)工程中使用的交流电器设备铭牌上标出的额定电压、电流的数值,交流电压表,电流表表面上标出的数字都是有效值。
对于正弦电流 ,代入式(5.5)得
,代入式(5.5)得
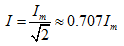 (5.6)
(5.6)
同理,正弦电压的有效值为
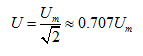 (5.7)
(5.7)
可见正弦量的有效值等于其最大值除以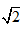 。
。
引入有效值的物理量后,正弦电流i又可表示为
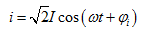 (5.8)
(5.8)
例5-3已知式(5.8)正弦电流在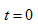 时,其瞬时值为8.66A,初相位
时,其瞬时值为8.66A,初相位 ,经过
,经过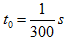 后电流值出现第一次下降为O的值。求
后电流值出现第一次下降为O的值。求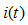 的有效值I,角频率
的有效值I,角频率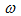 ,频率f和周期t。
,频率f和周期t。
解因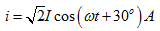 ,当
,当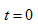 时,
时,
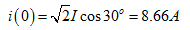
故有效值
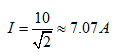
即
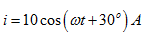
又
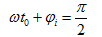
即
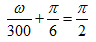
求得
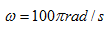
故
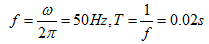
在线性定常电路中,如果全部激励都是同一频率的正弦量,则电路中的全部稳态响应也都是同一频率的正弦量,这意味着所求稳态响应的频率为已知量,不必再考虑。只要把正弦响应的其它两个要素,即最大值(或有效值)和初相位求出,则响应正弦量便完全确定。根据这一特点,可用一个复数来反映正弦量的幅值和初相位。这一复数称为正弦量的相量表示,简称为相量。例如正弦电流
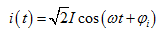
用相量表示记为
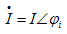 或
或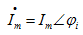 (5.9)
(5.9)
同理对于
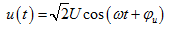
有
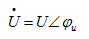 或
或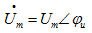 (5.10)
(5.10)
式中符号上加小黑点,是表示此复数专指正弦量而言,有别于其它复数。因此相量与正弦量之间存在一一对应关系。一个正弦量可以用有效值相量表示,也可以用最大值相量表示。
相量既然是复数,则可以在复平面上用有向线段表示。在复平面上相量的图示称为相量图。例如式(5.9)、式(5.10)的相量,表示在复平面上的相量如图5.5所示。可见,相量图不仅一目了然地表明了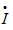 和
和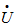 的有效值的大小和初相位,还显示了
的有效值的大小和初相位,还显示了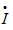 和
和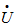 之间的相位关系。图上很直观地显示出
之间的相位关系。图上很直观地显示出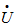 超前于
超前于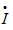 为
为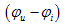 角度,或
角度,或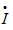 滞后于
滞后于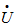 为
为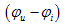 角度。
角度。
几点说明:
(1)相量用上面带点的大写字母表示。
(2)相量只用于表示正弦量(它包含了其对应正弦量的振幅(或有效值)和初相位两个要素),而不等于正弦量,即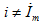 。
。
(3)代表正弦量的相量为一个复数,一般写为极坐标形式和指数形式,如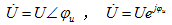 。也可以写成代数形式或三角形式,如
。也可以写成代数形式或三角形式,如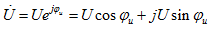 。
。
例5.4已知同频率电流为

试写出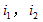 的相量表示式,画出相量图,并求
的相量表示式,画出相量图,并求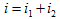 。
。
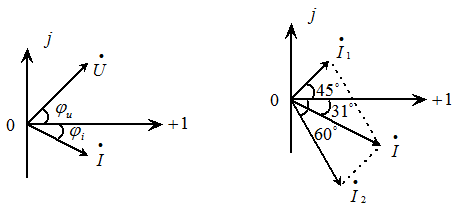
图5.5相量图图5.6
解: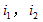 的相量为
的相量为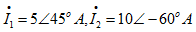 。相量如图5.6所示。因
。相量如图5.6所示。因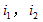 为同频率正弦量,故其和仍为一同频率正弦量,设
为同频率正弦量,故其和仍为一同频率正弦量,设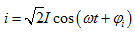 ,其相量
,其相量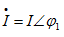 。则
。则
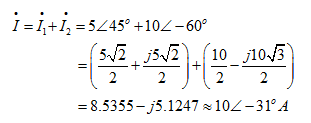
故
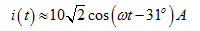
例5.5已知角频率为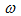 的正弦电压的相量为
的正弦电压的相量为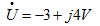 。试写出其时域表示式。
。试写出其时域表示式。
解:
故

在电路分析中,常常遇到正弦量的加、减运算和微分、积分运算,如果用与正弦量相对应的相量进行运算将比较简单。
例5.6如果有两个同频率的正弦电压分别为
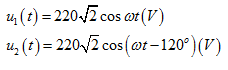
求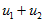 和
和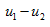 。
。
解:其所对应的相量分别为
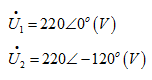
而相量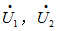 的和与差是复数加、减运算。可以求得
的和与差是复数加、减运算。可以求得
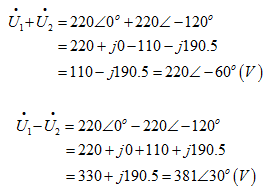
根据以上相量,可直接写出
