- 第一讲
- 第二讲
一.阻抗
对于图5.13 所示的
所示的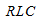 串联电路,若激励电压源
串联电路,若激励电压源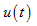 为正弦量,则可画出对应的频域向量模型,如图5.13(b)所示。由频域模型和向量形式的
为正弦量,则可画出对应的频域向量模型,如图5.13(b)所示。由频域模型和向量形式的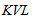 ,可得
,可得

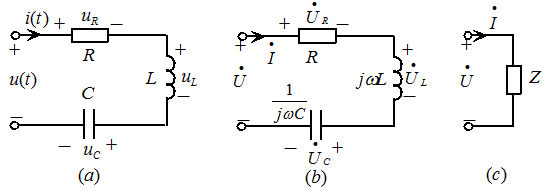
图5.13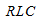 串联电路
串联电路
引入
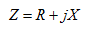 (5.18)
(5.18)
有
 (5.19)
(5.19)
式中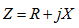 称为
称为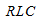 支路的频域阻抗或复数阻抗,简称阻抗,其实部为电阻部分,虚部
支路的频域阻抗或复数阻抗,简称阻抗,其实部为电阻部分,虚部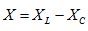 称为电抗。Z和R,X的单位均为
称为电抗。Z和R,X的单位均为 。式(5.19)称为相量形式的欧姆定律,其频域模型如图5.13(c)所示。
。式(5.19)称为相量形式的欧姆定律,其频域模型如图5.13(c)所示。
阻抗是一个复数,故也可写为
 (5.20)
(5.20)
式中,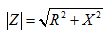 称为阻抗的模(或大小);
称为阻抗的模(或大小); 称为阻抗的辐角,也称为阻抗角。可以看出,阻抗模
称为阻抗的辐角,也称为阻抗角。可以看出,阻抗模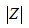 ,电阻R及电抗X在数值上符合直角三角形关系,如图5.14(a)所示。此直角三角形称为阻抗三角形。若阻抗三角形的各边乘以
,电阻R及电抗X在数值上符合直角三角形关系,如图5.14(a)所示。此直角三角形称为阻抗三角形。若阻抗三角形的各边乘以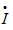 ,则对应为电阻、电抗及复阻抗上的电压
,则对应为电阻、电抗及复阻抗上的电压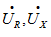 和
和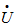 ,如图5.14(b)所示,此直角三角形称为电压三角形。
,如图5.14(b)所示,此直角三角形称为电压三角形。
由式(5.20),有
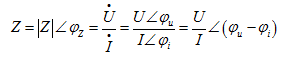
可见,阻抗模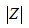 为电压有效值与电流有效值I之比,即
为电压有效值与电流有效值I之比,即 ;阻抗角
;阻抗角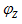 反映电压
反映电压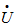 与电流
与电流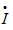 的相位差角,即
的相位差角,即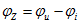 。
。

图5.14
需要强调的是,阻抗虽是复数,但它与相量不同。相量表示正弦量,而阻抗仅反映电路频域的性质,不代表正弦量,所以在Z上不加小黑点,以便与相量相区别。事实上,对于 ,由于X与电路的工作频率有关,故对应频率不同,X也不同,即电路性质不同。当
,由于X与电路的工作频率有关,故对应频率不同,X也不同,即电路性质不同。当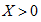 时,
时,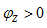 ,
,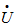 超前
超前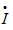 ,电路对外呈电感性;当
,电路对外呈电感性;当 时,
时,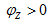 ,
,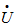
滞后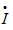 ,电路对外呈电容性;当
,电路对外呈电容性;当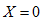 时,
时, ,
,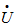 与
与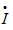 相同,电路对外呈电阻性,这种现象称之为谐振现象。
相同,电路对外呈电阻性,这种现象称之为谐振现象。
二.导纳
对于同一支路,定义阻抗Z的倒数为复导纳,简称导纳,即
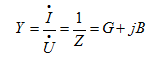 (5.21)
(5.21)
单位为西门子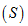 。其中
。其中 为导纳的电导,
为导纳的电导,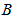 为导纳的电纳,一般电纳由两部分组成,即
为导纳的电纳,一般电纳由两部分组成,即
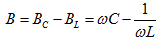 (5.22)
(5.22)
式中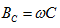 称之为容纳,
称之为容纳,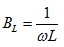 称之为感纳。
称之为感纳。
导纳的物理意义为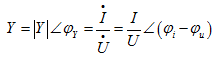 ,故
,故

即 等于电流与电压有效值之比,且与
等于电流与电压有效值之比,且与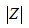 互倒;
互倒;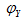 是电流
是电流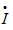 与电压
与电压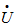 的相位差角,
的相位差角,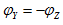 。
。
与Z类似,导纳的模 ,电导
,电导 和电纳
和电纳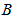 也可以组成一个直角三角形,此三角形称为导纳三角形。
也可以组成一个直角三角形,此三角形称为导纳三角形。
值得注意的是,当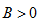 时,
时,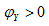 ,电路对外呈电容性,
,电路对外呈电容性,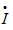 超前
超前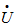 ;当
;当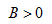 时,
时,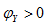 ,电路对外呈电感性,
,电路对外呈电感性,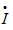 滞后
滞后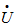 ;当
;当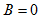 时,
时, ,电路对外呈电阻性,
,电路对外呈电阻性,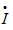 与
与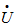 相同,并出现谐振。
相同,并出现谐振。
由于Z和Y都同样地表征了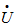 和
和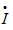 之间的大小和相位关系,因此两者是相互等效的。这样,对于同一个支路即可用Z表示,也可用Y表示。
之间的大小和相位关系,因此两者是相互等效的。这样,对于同一个支路即可用Z表示,也可用Y表示。
对于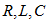 单个元件,其阻抗和导纳分别为
单个元件,其阻抗和导纳分别为
电阻元件: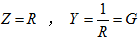 。
。
电感元件: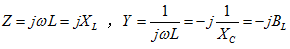 。
。
电容元件: 。
。
例5.10图5.15 所示电路,已知
所示电路,已知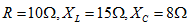 ,电路两端电压
,电路两端电压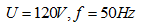 。求电路的导纳;电流,
。求电路的导纳;电流,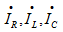 及总电流
及总电流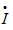 ;画出相量图。
;画出相量图。
解:设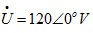 。导纳
。导纳

电 流
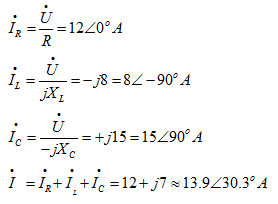
或
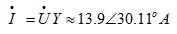
其相量图为图5.15(b)所示。
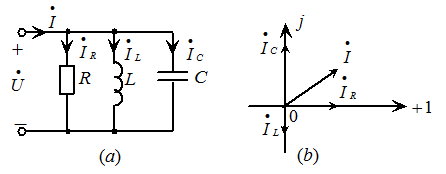
图5.15