含有电感L、电容C的无源单口网络在正弦激励作用下,可以在一个或若干个频率上出现端口电压、电流同相位的现象，这种现象称之为谐振现象。发生谐振现象的电路，统称为谐振电路。在电子和无线电力工程中，经常要从许多电信号中选取出我们所需要的电信号，而同时把我们不需要的电信号加以抑制或滤处，为此就需要一个选择电路，即谐振电路。

由前面分析可知，线性无源的单口网络（或电路），可以等效为一个阻抗或导纳，因此谐振的条件是

（5.45）

或

（5.46）

谐振分为简单谐振和复杂谐振两类。简单谐振包括串联谐振和并联谐振，复杂谐振包括串并谐振和耦合谐振。我们只研究简单谐振的一些基本概念。

一.串联谐振

图5.31

由电感和电容串联而组成的电路，图8.31所示，其中为电路的总电阻，由式（5.45）可知，当时，即有，即与相同。此时我们就说电路发生了谐振。

电路达到谐振的条件为

（5.47）

由此可得

（5.48）

称为电路的固有谐振角频率，简称谐振角频率，因为它只由电路本身的参数，所决定。电路的谐振频率则为

（5.49）

式（5.48）表明，当电源的角频率与电路的固有谐振角频率相等时，电路即发生谐振。

电路在谐振时的输入阻抗称为谐振阻抗，用表示。由于谐振时的电抗，故谐振阻抗为

（5.50）

可见为纯电阻，且其值为最小。

谐振时的感抗和容抗称为电路的特征阻抗，用表示。即

（5.51）

可见只与电路参数，有关，而与无关，且有。

品质因数用表示，定义为特征阻抗与电路的总电阻之比，即

（5.52）

在电子工程中，值一般在之间。

谐振阻抗的又一表示式为

（5.53）

因此，串联谐振电路在谐振时的特性有：

谐振阻抗为纯电阻，其值为最小，即。

电流与电源电压同相位，即。

电流的模达到最大值，即。称为谐振电流。

和两端均可能出现高电压，即

（5.54）

（5.55）

可见当时，即有，故串联谐振又称为电压谐振。这种出现高电压的现象，在无线电和电子工程中极为有用，但在电力工程中却表现为有害，应予防止。

例5.21一半导体收音机的输入电路为，，串联电路，，。当收听频率的电台广播时，输入信号电压的有效值。求可变电容的值、电路的值和输出电压的值。

解：

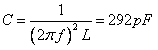
二.并联谐振电路

如图5.32并联电路，为电流源的电流。由式（5.46）可知，当时，即有，即与相同。此时我们就说电路发生了并联谐振。

图5.32

电路的导纳

而电路达到谐振的条件为

（5.56）

由此可得

（5.57）

称为电路的固有谐振角频率，简称谐振角频率，因为它只由电路本身的参数，所决定。电路的谐振频率则为

（5.58）

式（5.58）表明，当电源的角频率与电路的固有谐振角频率相等时，电路即发生了并联谐振。

并联谐振时，谐振导纳最小，其谐振阻抗为，，其值为最大。

同理，特征阻抗

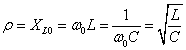
品质因数用表示，定义为谐振时的感纳或容纳与电路的总导纳之比，即

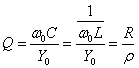
（5.59）

因此，并谐振电路在谐振时的特性有：

（1）谐振导纳为纯电导，其值为最小，即。谐振阻抗，其值为最大。

（2）电流与电压同相位，即。

（3）输出电压达到最大值，即

（4）和中的电流大小相等，相位相反，故。

（5）和中均可能出现高电流，即

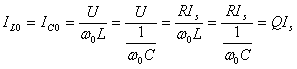
可见当时，即有，故并联谐振又称为电流谐振。