图1　　写出图1所示各电路的时域伏安关系和频域伏安关系，其中右边的电路为左边电路的相量电路模型。

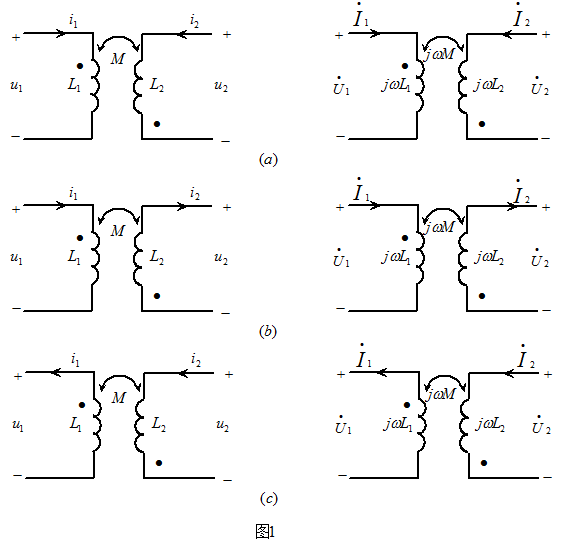
解:　　　

　　　　　　(a)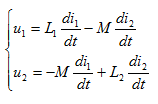

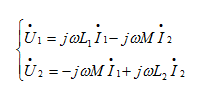
　　　　　　(b)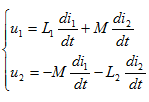

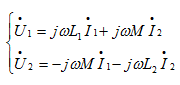
　　　　　　(c)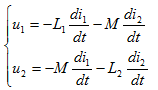

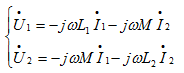
图2　　求图2所示电路的端口等效电感L。

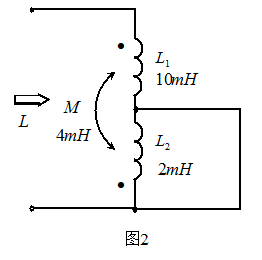
解:　　下图为此电路的去藕等效电路，故得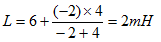

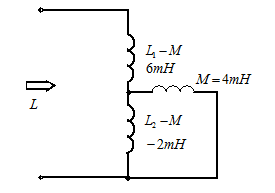
图3　　所示的电路，求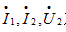及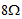电阻消耗的平均功率P。

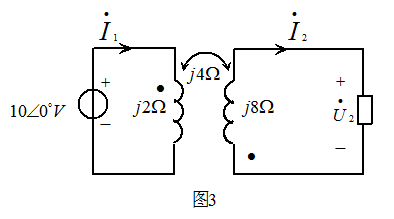
解:　　用直接法求解。该电路的ＫＶＬ方程为

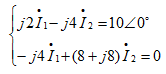
　　　　　　解之得：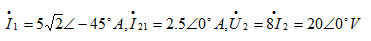 

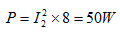
1. 图4　　所示电路，求ａ、ｂ端口的输入电阻。

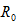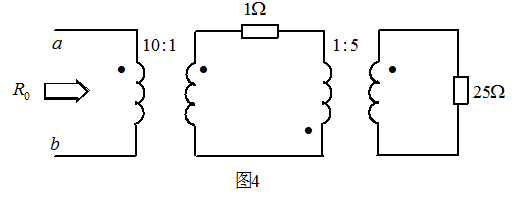
解:　　将原图按照下图（ａ）、（ｂ）依次进行等效变换，可得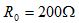

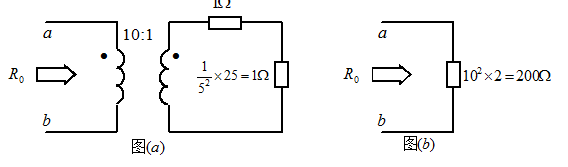
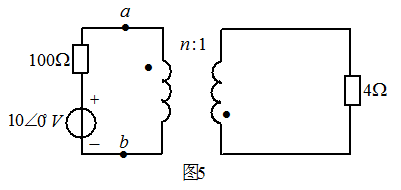
1. 图5　　所示电路，欲使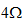电阻获得最大功率，求变比ｎ，并求最大功率。

解:　　ａ、ｂ端的输入电阻为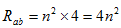，故得等效电路如下图示：

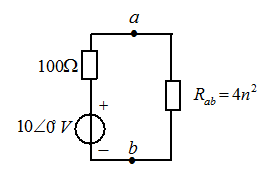
　　　　　根据最大功率传输定理，当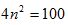时功率最大，即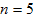，且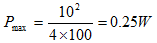

图6　　所示电路，已知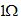电阻吸收的功率为１０Ｗ，求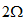电阻所吸收的功率。

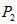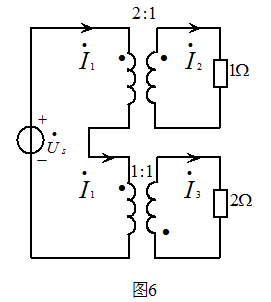
解: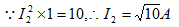　　

　　　　　　　　又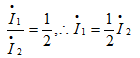

　　　　　　　　又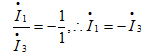

　　　　　　　　所以，

　　　　　　　　故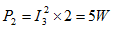

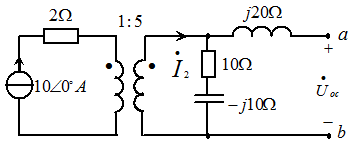
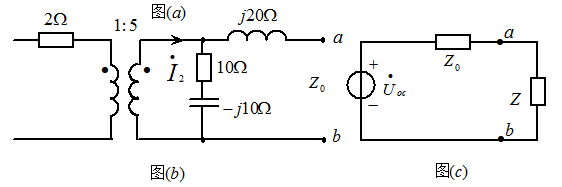
1. 图7　　所示电路，求阻抗Ｚ为何值时可获得最大功率，并求最大功率的值。

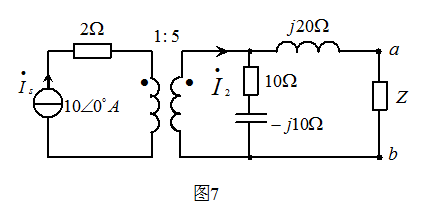
解:　　用戴维南定理求解。

1. 　　　　　　(1)如下图（ａ）所示，可求得端口的开路电压。

。

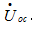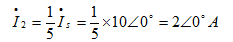
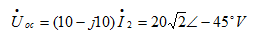
　　　　　　(2)根据图（ｂ）可求得端口的输入阻抗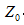

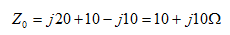
　　　　　　(3)可画出等效电压源电路如图（ｃ）所示。根据最大功率传输定理可知，当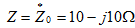时可获得最大功率，且。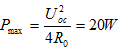