一.定义与电路符号

理想变压器也是一种理想的电路元件。为了易于理解，我们耦合电感的极限情况来引出它的定义。

图7.13是耦合电感的原理结构与磁场分布，，分别为初级与次级线圈的匝数。定义，n称为变比，也称匝数比。

图7.13理想变压器的定义与电路符号

理想变压器的理想化条件：

（1）无漏磁通，即,耦合系数K=1，为全耦合，故有，。

（2）不消耗能量（即无损失），也不贮存能量。

（3）初、次级线圈的电感均为无穷大，即→∞，→∞，但为有限值。即在全耦合（K=1）时，两线圈的电感之比，是等于其匝数平方之比。

（4）因有K=1，→∞，→∞,故有→∞。

满足以上四个条件的耦合电感称为理想变压器。可见理想变压器可认为是耦合电感的极限情况。即K=1，→∞，→∞,M→∞的情况，它纯粹是一种变化信号的传输电能的元件，但它与耦合电感在本质上已不同了。耦合电感是依据电磁感应原理工作的，是动态元件，需要3个参数，，来描述；而理想变压器已没有了电磁感应的痕迹，是静态元件，只需要一个参数来描述。理想变压器的电路符号如图7.13所示。

二.伏安方程

从图7.13看出，由于无漏磁通，故穿过两个线圈的总磁通相同，均为。又由于图中,和三者的参考方向互为关联，,和三者的参考方向也互为关联，故

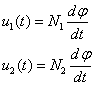
故有（7.10）

或（7.11）又因为理想变压器不消耗也不贮存能量，所以它吸收的瞬时功率必为零，即必有

故得

（7.12）

或　　　　　　　　　　　　　　　　　　　（7.13）

式（7.10）至（7.13）即为理想变压器的时域伏安方程。可看出：

（1）由于n为大于零的实数，故此两方程均为代数方程。即理想变压器为一静态元件（无记忆元件），已经没有了电磁感应的痕迹，所以能变化直流电压和直流电流。

（2）理想变压器的两线圈的电压与其匝数成正比，两线圈的电流与其匝数成反比，且当时有，为升压变压器；当时有，为降压变压器；当是有，既不升压也不降压。

（3）在电路理论中，我们把能联系两种电路变量的元件称为相关元件，否则即为非相关性元件。电阻、电感、电容等均为相关性元件，而理想变压器则为非相关性元件，亦即与之间，与之间，均无直接的约束关系，它们均各自由外电路决定。

当电路工作在正弦稳态时，式（7.10）至（7.13）即可写为相量形式，即

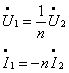
（7-11）

式（7.10）至（7.13）均是在图7.13所示电压参考极性与电流参考方向以及同名端标志下列出的。若线圈的同名端或电压的参考极性，电流的参考方向改变了，则其伏安方程中等号右端的“·”，“-”号也应相应改变。

例如对于图7.14所示电路，则其伏安方程为

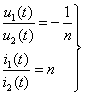或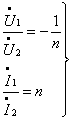

图7.14理想变压器电路

对于图7.15所示电路，则其伏安方程为

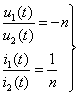或

图7.15理想变压器

 三.阻抗变换

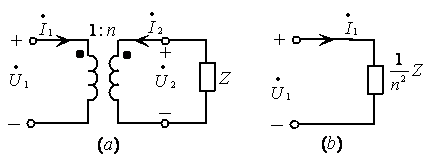
图7.16理想变压器的阻抗变换作用

设在理想变压器的次级接阻抗，如图7.16所示，则因有

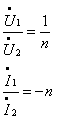
故得原边的输入阻抗为

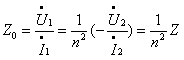(7.12)

于是可得原边等效电路如图7.1所示。从式（7.12）看出：

（1）n≠1时，。这说明理想变压器具有阻抗变换作用。

  （2）由于n为大于零的实常数，故与的性质全同，即次级的R，L，C，变换到初级相应为,,。

  （3）阻抗变换与同名端无关。

  （4）当Z=0时，则=0，即当次级短路时，相当于初级也短路。

  （5）Z=∞时，则=∞，即当次级开路时，相当于初级也开路。

  （6）阻抗变换具有可逆性，即也可将原边的阻抗Z变换到副边，如图7.17所示。但要注意此时副边的等效阻抗为。

图7.17阻抗变换作用的可逆性

⑺阻抗在某一边是串联（并联），则变换到另一边也是串联（并联），如图7.18所示。

图7.18理想变压器阻抗变换作用的性质

由以上的全部叙述可见，理想变压器既能变换电压和电流，也能变换阻抗，因此，人们更确切地称它为变量器。

五.含理想变压器电路的分析计算

含理想变压器电路的分析计算，一般仍是应用回路法（网孔法）和节点法等方法，只是在列方程时，必须充分考虑它的伏安关系和阻抗变换特性即可解决问题。

例7.5图7.19所示电路，欲使电阻获得最大功率，求变比，并求最大功率。

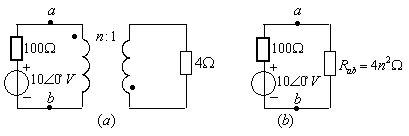
图7.19

解：ａ、ｂ端的输入电阻为，故得等效电路如下图7.19示：

根据最大功率传输定理，当时功率最大，即，且

例7.６．图7.20所示电路，已知电阻吸收的功率为，求电阻所吸收的功率。

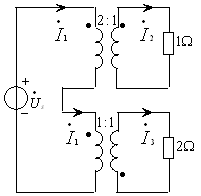
图7.20

解：

又　

所以

，

故　　　　　　　　　　　　　　　　　　　　　　　

例7.7图7.21所示电路，求阻抗Ｚ为何值时可获得最大功率，并求最大功率的值。

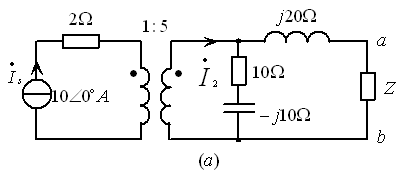
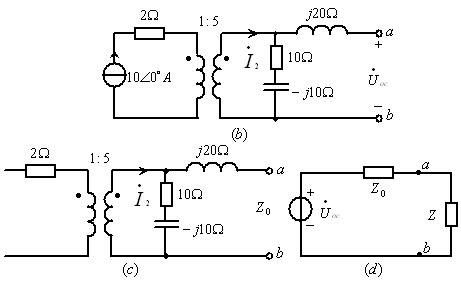
图7.21

解：用戴维南定理求解。

（１）如图7.21所示，可求得端口的开路电压。

（２）根据图7.21可求得端口的输入阻抗。

（３）可画出等效电压源电路如图7.21所示。根据最大功率传输定理可知，当时可获得最大功率，且。

例7.8图7.22电路，已知，V,求,,。

图7.22

解：

设理想变压器两边的电压分别为,,则可列出方程

又有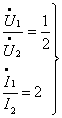　　　　　　　　　　　　　　　　　　　　

以上五式联解即得

A，A，A