线性非正弦周期电流电路稳态分析的一般步骤如下:
(1)将给定的激励源[例如电压源![]() ]展开成傅里叶级数,即
]展开成傅里叶级数,即
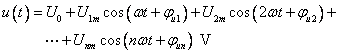
这样,电压源![]() 的作用,就与一个直流电压源
的作用,就与一个直流电压源![]() 及许多具有不同频率的正弦电压源串联起来共同作用在电路中的情况全同,如图8.4
及许多具有不同频率的正弦电压源串联起来共同作用在电路中的情况全同,如图8.4![]() 和
和![]() 所示。其中
所示。其中
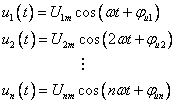
(2)根据叠加定理,可将图8.4![]() 分解成图8.4
分解成图8.4![]() 的叠加。
的叠加。
(3)根据图![]() ,分别求直流分量
,分别求直流分量![]() 与争先稳态响应电流
与争先稳态响应电流![]() ,
,![]() ,
,![]() 。求解时可用相量法,其相应的频域电路(即相量模型)如图
。求解时可用相量法,其相应的频域电路(即相量模型)如图![]() ,
,![]() ,
,![]() ,
,![]() 所示。于是得
所示。于是得
![]()
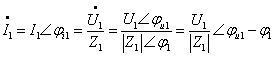
其中![]() ,
,![]() 为一次谐波电压的相量;
为一次谐波电压的相量;
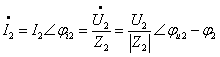
其中![]() ,
,![]() 为二次谐波电压的相量;
为二次谐波电压的相量;
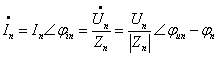
其中![]() ,
,![]() 为
为![]() 次谐波电压的相量。因此,其对应的各次谐波的正弦稳态响应电流为
次谐波电压的相量。因此,其对应的各次谐波的正弦稳态响应电流为
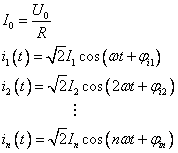
其中 ![]() 。
。
将以上结果相加,即得非正弦周期稳态响应电流,即
![]()
但要切记 ![]()
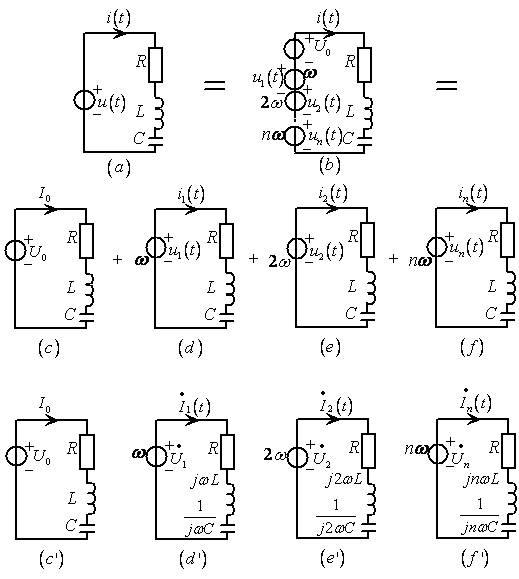
图8.4非正弦周期电流电路稳态分析
具体求解时注意:
(1)当直流分量作用时,电感相当于短路,电容相当于开路,只分析纯电阻电路。
(2)当谐波分量作用时,由于激励都是正弦电源,因此可用相量法求解各响应分量。但必须注意,这里各正弦电源具有不同频率,故电路中电抗元件对各次谐波的阻抗也不同。次谐波的感抗是基波感抗![]() 的
的![]() 倍,
倍,![]() 次谐波的容抗是基波容抗
次谐波的容抗是基波容抗![]() 的
的![]() 分之一。
分之一。
(3)由于不同频率的正弦量不能用相量法相加,故求出各相应分量后,应写成瞬时表达式,在时域中进行叠加。
例8.4图![]() 中,已知
中,已知![]() ,电路对基波的阻抗
,电路对基波的阻抗![]() 。求稳态电流
。求稳态电流![]() 。
。
解:
对基波: ![]()
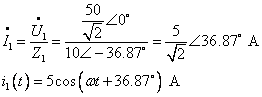
对第三次谐波: ![]()

故
![]()
例8.5图![]() 所示电路,已知
所示电路,已知![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 。求两个电流表的读数和
。求两个电流表的读数和![]() ,
,![]() 。
。
 图8.5
图8.5
解:按图![]() 求直流分量,即
求直流分量,即
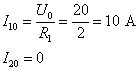
按图![]() 求一次谐波电流,其频域电路如图
求一次谐波电流,其频域电路如图![]() 所示。设
所示。设![]() ,初、次级电流为
,初、次级电流为![]() ,
,![]() ,则可列出
,则可列出![]() 方程为
方程为
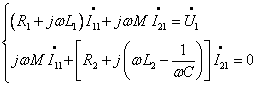
代入数据解之得

故得 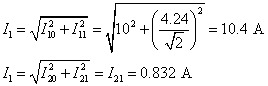
即电流表![]() 的读数为
的读数为![]() ,
,![]() 的读数为
的读数为![]() 。其表达式为
。其表达式为

例8.6图8.6电路,已知![]() 。今欲使
。今欲使![]() ,求
,求![]() 和
和![]() 值。
值。

图8.6
解:应使![]() ,
,![]() 对
对![]() 发生串联谐振,同时使
发生串联谐振,同时使![]() ,
,![]() 和
和![]() 对
对![]() 发生并联谐振。故有
发生并联谐振。故有

联解得 