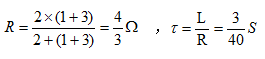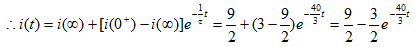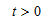您的当前位置:课程学习 > 第九章 > 本章例题
图1 所示电路,已知t<0时开关S打开,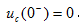 。t=0时刻闭合开关S,求
。t=0时刻闭合开关S,求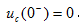 。
。
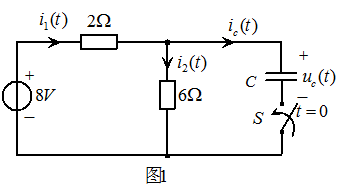
解: t=0时S闭合,则有
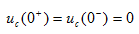
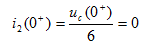
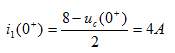
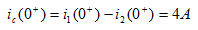
图2 所示电路,已知t<0时开关S闭合,电路已达稳态。t=0时刻打开开关S,求t>0时的响应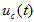 和
和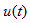 。
。
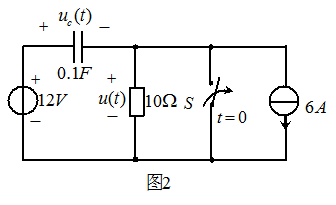
解: t<0时开关S闭合,电路已达稳态,电容C相当于开路,因此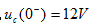 。
。
t=0时刻打开开关S,有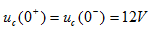
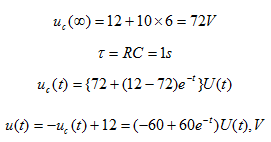
图3 所示电路,已知t<0时开关S在“1”的位置,电路已达稳态。t=0时刻将开关S扳到“2”的位置。求t>0时的响应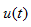 。
。
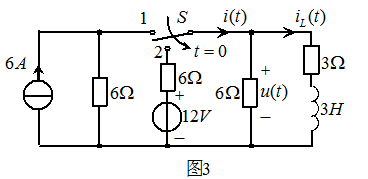
解: t<0时开关S在“1”的位置,电路已达稳态,电感相当于短路,有
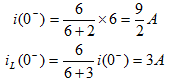
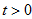 时开关S在“2”的位置,有
时开关S在“2”的位置,有
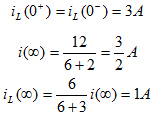
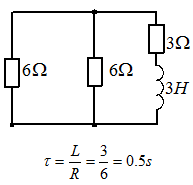
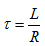 ,其中R可由下图求得,
,其中R可由下图求得,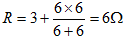
故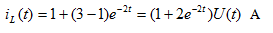 A
A
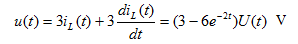 V
V
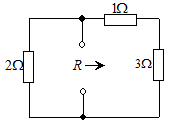
- 图4 所示电路,已知t<0时开关S打开,电路已达稳态。t=0时刻将开关S闭合。求t>0时的响应
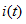 。
。
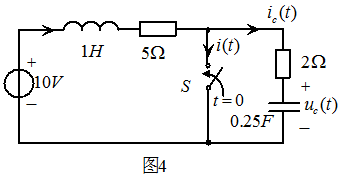
解: t<0时开关S打开,电路已达稳态,电容C相当于断路,电感L相当于短路,有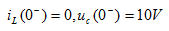
t>0时S闭合,有
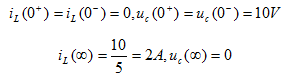
t>0时有两个相互独立的回路,时间常数
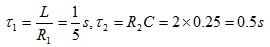
故
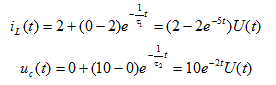
所以
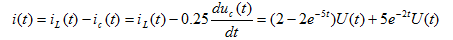
- 图5 所示电路,激励
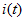 的波形如右图所示,求零状态响应
的波形如右图所示,求零状态响应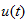 。
。
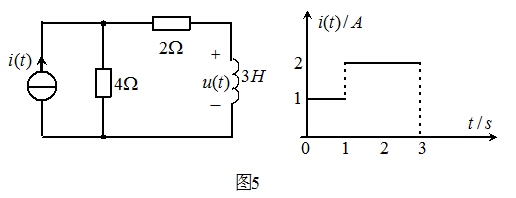
解: 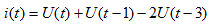 A
A
当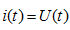 单独作用时,可求得电感电压的零状态响应
单独作用时,可求得电感电压的零状态响应
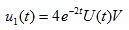
根据线性电路的性质得
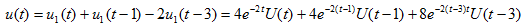 V
V
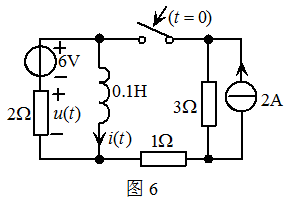
图6 电路中,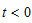 时开关打开,电路已达稳定;
时开关打开,电路已达稳定;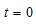 时闭合开关。求
时闭合开关。求 时时的
时时的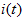 和
和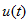 。
。
解: 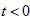 时,开关打开,电路已达稳定:
时,开关打开,电路已达稳定: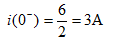
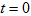 时闭合开关,由换路定律得:
时闭合开关,由换路定律得: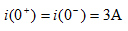
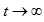 时的等效电路为:
时的等效电路为: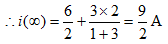
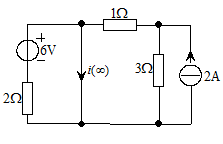
如下图示: