时刻电路中的电压、电流以及它们的各阶导数的值统称为电路电量的初始值。电路初始值的求法：

（1）根据换路前的电路，求出及。

（2）根据换路定律求出及。

（3）画出时的等效电路。其中电容用电压等于的电压源代替，电感用电流等于的电流源来代替。

（4）根据时的等效电路（电路已无动态元件），求出电路中待求电压和电流的初始值。

几点说明：

（1）用经典法求解微分方程时，须根据电路变量的初始值确定解答中的积分常数。把电容电压的初始值和电感电流的初始值称为独立的初始值，其余的称为非独立的初始值。

（2）换路定律只适于求储能元件电容电压和电感电流的初始值，不能用于直接求其他变量的初始值。

（3）若电容电流和电感电压为无穷大时，不能应用换路定律求和，需用电荷守恒求，用磁链守恒求，本书不予研究。

例9.1如图9.8所示电路，已知时开关打开，。现时将开关闭合，求。

图9.8

解：

时，打开，。

时，闭合，由换路定理可知：

因此，画出其时的等效电路，如图9.8所示，有

例9.2如图9.9所示电路，时开关在“1”，电路已处于稳定状态。现时将开关从“1”扳到“2”，求。

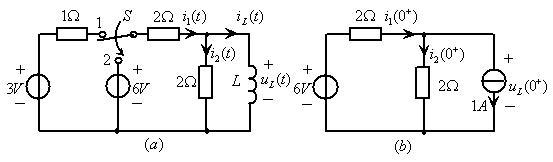图9.9

解：

时开关在“1”，电路已处于稳定状态，电感相当于短路，有

开关在“2”，根据换路定理有，因此，时刻的等效电路如图9.9所示，根据KVL、KCL有

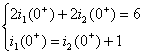
解之得　　　　　　　　　　　

例9.3图9.10所示电路，时闭合，电路已达稳态。今于时刻打开，求初始值。

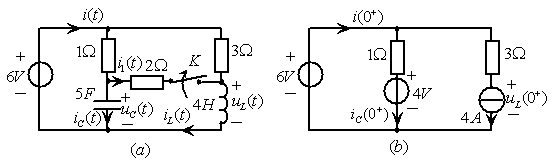图9.10

解：

该电路中的激励为恒定激励。在恒定激励下，当电路达到稳定状态时，电路中的电容相当于开路，电感相当于短路。时，闭合，电路中的电容相当于开路，电感相当于短路。故根据图9.10有

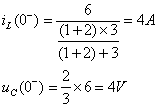
时刻打开，故根据换路定律有

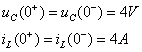
时刻的等效电路如图9.10所示，有

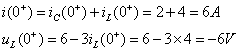
又因有　　　　　　　　　　　　　，

故得