一.电路

1.电路的零输入响应

   外加激励为零但初始条件不为零的电路称为零输入电路。仅由初始条件激励所产生的响应称之为零输入响应。

   图9.17为串联的零输入电路，设初始条件。故时电路中的，和即均为零输入响应。

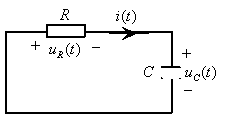
图9.17RC零输入电路

根据KVL有

即

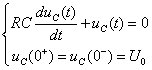
这是一个待求变量为的一阶线性常系数齐次微分方程。其特征方程为

故得方程的特征根（也称电路的固有频率或自然频率）为

其中，单位为秒，称为电路的时间常数。

故得电路方程的解为

(9.10)

根据式（9.10）画出的的波形如图9.18所示。可见为一随时间t而衰减的指数曲线，衰减的快慢取决于的大小，大衰减的慢，小衰减的快。

电路从一种稳定状态变换到另一种新的稳定状态，其间所经历的过程称为瞬态过程。由式（9.10）看出，当t=∞时有。称为的稳态值。但实际上，当时，即有，即经历的时间，我们即认为电路已达到了新的稳定状态。

图9.18电路的零输入响应

响应电流和响应电压分别为

或写成下面的形式，即

和的波形分别如图9.18所示。

2.电路的零状态响应

初始条件为零的电路称为零状态电路。仅由外加激励在零状态电路中产生的响应称为零状态响应。

图9.19所示电路，时开关在“2”，电路稳定，此时。当时将开关从“2”扳到“1”，为直流电压源电压。

图9.19零状态电路

根据可列出时的方程为

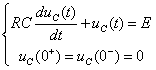
这是一个待求变量为的一阶线性常系数非齐次常微分方程，其特征方程为

故得方程的特征根（即电路的固有频率或自然频率）为

其中为电路的时间常数。

故可得方程的解为

(9.11)

的波形如图9.20所示。可见为一随时间t而增长的指数曲线，增长的快慢取决于电路时间常数的大小，大增长的慢，小增长的快。

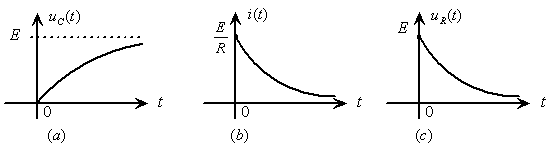
图9.20电路的零状态响应

在理论是，当t→∞时，，但实际上，当时，即有，即认为经历的时间后，电容器C的充电即告完成，电路即达到了新的稳定状态。

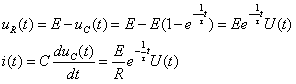
和的波形分别如图9.20、所示。

二.电路

1.零输入响应

图9.21所示电路，已知时开关在，电路稳定。今于时刻将从扳到，并设初始条件，求时的响应、。很显然，、均为电路的零输入响应。

根据列出时的方程为

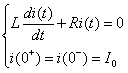
图9.21零输入电路

这是一个待求变量为的一阶线性常系数齐次常微分方程，其特征方程为

故得特征根为

其中，单位为秒(s)，称为电路的时间常数。

故得电路方程的解为

(9.12)

的波形如图9.22所示。可见为一随时间t而衰减的指数曲线，衰减的快慢取决于的大小。

图9.22电路的零输入响应

响应电压为

的波形如图9.22所示。

2.零状态响应

图9.23所示电路，已知时开关在，电路稳定。今于时刻将从扳到，初始条件。求时的响应、。很显然，、均为电路的零状态响应。

根据列出时的方程为

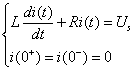
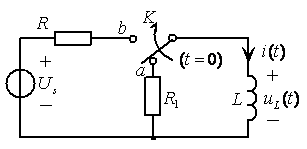
图9.23零状态电路

这是一个待求变量为的一阶线性常系数非齐次常微分方程，故得电路方程的解为

(9.13)

的波形如图9.24所示。可见为一随时间按指数规律上升的曲线，上升的快慢取决于的大小。

响应电压为

的波形如图9.24所示。

图9.24电路的零状态响应