若电路中既有外加激励且初始条件（即内激励）也不为零，则电路中产生的响应称为全响应。即外加激励与内激励共同产生的响应，称为全响应。

图9.25(a)为非零状态的串联电路，其外加激励为阶跃电压，并设电路的初始条件为。

根据叠加原理，我们可将图9.25(a)所示电路分解成图9.25(b)所示零输入电路与图9.25(c)所示零状态电路的叠加。于是图9.25(a)电路中的全响应，即等于图9.25(b)电路中的零输入响应与图9.25(c)电路中的零状态响应的叠加，即

零输入响应零状态响应

将式（9.10）和（9.11）所示结果代入上式即得全响应为

图9.25电路的全响应

（9.14）

由式（9.14）可得

（9.15）

其中，即为电容的稳态电压，即当时电容电压。电容的初始值。

于是，对于一阶电路，只要求得了、和这三个要素值，然后代入此式，即可得电路的全响应。

式（9.15）推广，对于一阶电路中的任何变量，此式都成立。故可写为一般性的公式，即

　　（9.16）

其中，为稳态值，即当时电路的响应，由时的稳态电路求解；为初始值，可根据换路定理和等效电路求得；或为电路的时间常数，单位为秒，其中是从动态元件两端看进去的戴维南等效电阻。

几点说明：

（1）三要素公式只适应于一阶电路；

　　（2）只适用于直流激励或阶跃激励；

　　（3）不论那个变量，只要是同一电路的，其时间常数相同；

（4）三要素公式不仅能求零状态响应，也能求零输入响应及全响应。

例9.3图9.25所示电路，已知t<0时开关S闭合，电路已达稳态。t=0时刻打开开关S，求t>0时的响应和。

图9.25

解：

t<0时开关S闭合，电路已达稳态，电容C相当于开路，因此。

t=0时刻打开开关S，有

例9.4图9.26所示电路，已知t<0时开关S在“1”的位置，电路已达稳态。t=0时刻将开关S扳到“2”的位置。求t>0时的响应。

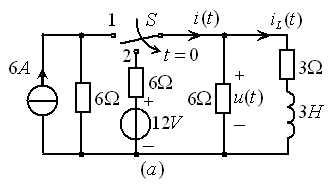
图9.26

解：

t<0时开关S在“1”的位置，电路已达稳态，电感相当于短路，有

时开关S在“2”的位置，有

，其中R可由图9.26求得，

故　　　　　　　　　　　　　　　A

V

例9.5图9.27所示电路，已知t<0时开关S打开，电路已达稳态。t=0时刻将开关S闭合。求t>0时的响应。

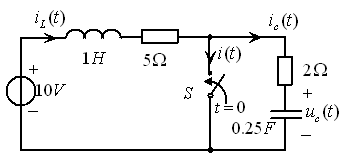
图9.27

解：

t<0时开关S打开，电路已达稳态，电容C相当于断路，电感L相当于短路，有

t>0时S闭合，有

t>0时有两个相互独立的回路，时间常数

故

所以

例9.6图9.28所示电路，激励的波形如右图所示，求零状态响应。

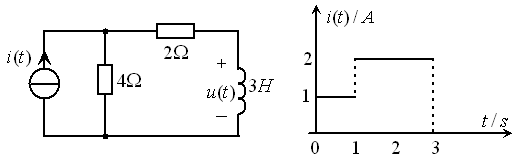
图9.28

解：　　　　　　　　　　　　　　　　A

当单独作用时，可求得电感电压的零状态响应

根据线性电路的性质得

V

例9.7如图9.29所示电路，已知，求电压，电流。

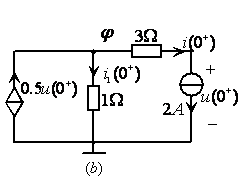
图9.29

解：

（1）时的等效电路如图9.29所示，其中，有

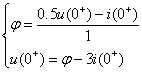
所以　　　　　　　　　　　　　　

　　　故　　　　　　　　　　　　

（2）时，Ｌ短路，故。

（３）如图9.29所示，求时间常数。

　因为　　　　　　　　　　　　　

　所以　　　　　　　　　　　　　，

于是