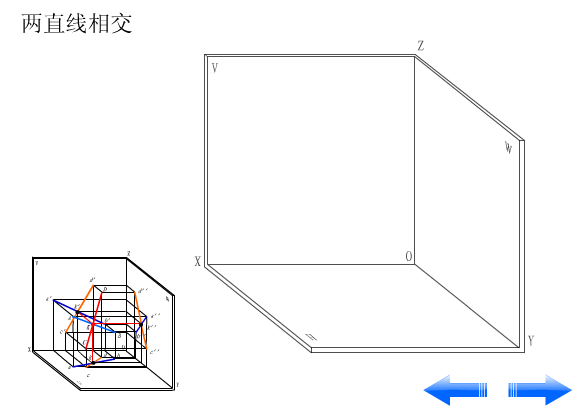
直线(线段)的投影一般仍然是直线(线段),特殊情况下可以积聚为一点。
直线三面投影与点三面投影的关系?
直线相对于三个投影面的位置关系有三种:平行、垂直和倾斜
1.平行于一个投影面的直线称为投影面的平行线
2.垂直于一个投影面的直线称为投影面的垂直线
3.倾斜于三个投影面的直线称为一般位置直线
直线与投影面之间的夹角称为倾角。直线对H,V,W三个投影面的倾角分 别规定用α、β、γ表示
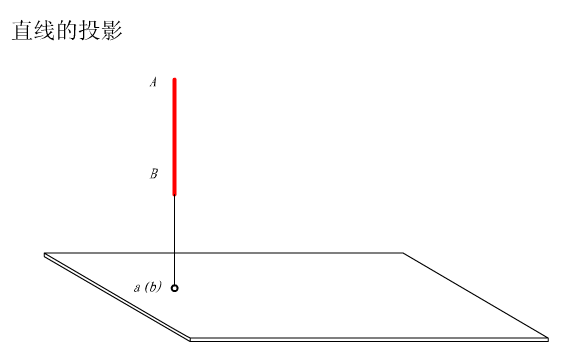

直线的投影及倾角
2.4.1 各种位置直线的投影规律
1.投影面的平行线
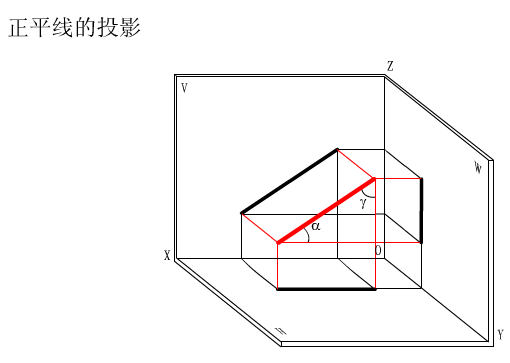
投影面的平行线根据具体平行于哪一个投影面,又分为水平线、正平线和侧平线。
投影面的平行线的投影特性:
(1)投影面的平行线在其平行的投影面上的投影反映实长,并且与投影轴的夹角等于空间直线对相应投影面的倾角。
(2)其他两面投影均小于实长,且分别平行于相应的投影轴。

2.投影面的垂直线
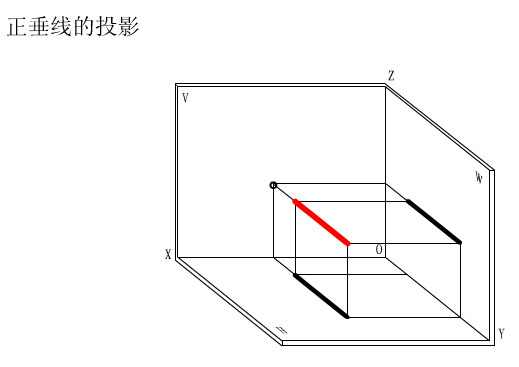
投影面的垂直线根据具体垂直于哪一个投影面,又分为铅垂线、正垂线和侧垂线。
投影面的垂直线的投影特性:
(1)投影面的垂直线在其所垂直的投影面上的投影积聚为一 点;
(2)其他两面投影垂直于相应的投影轴,且反映实长;
(3)空间直线对三个投影面的倾角为 0 度或 90 度。

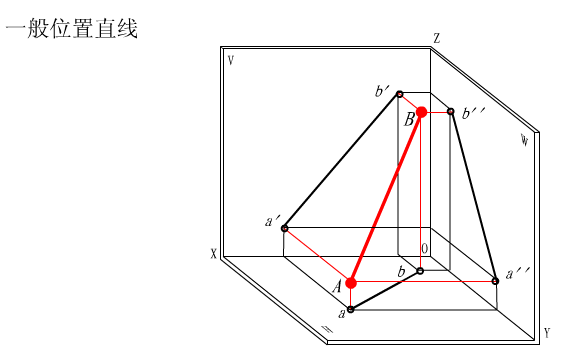
3.一般位置直线
一般位置直线对三个投影面都倾斜,因此三面投影都小于实长;三个投影与投影轴都倾斜;三个投影与投影轴的夹角也不反映空间直线与投影面的三个倾角α、β、γ 。

2.4.2 求一般位置直线的实长及倾角
1、直角三角形法

2.更换投影面法(换面法)


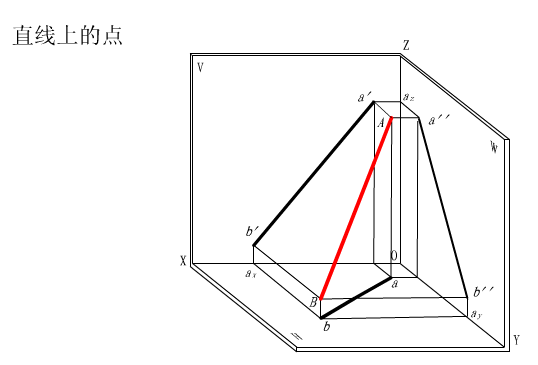
2.4.3 直线上的点
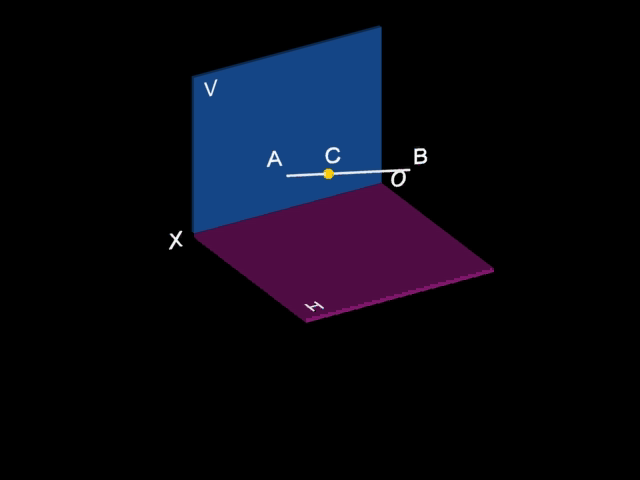
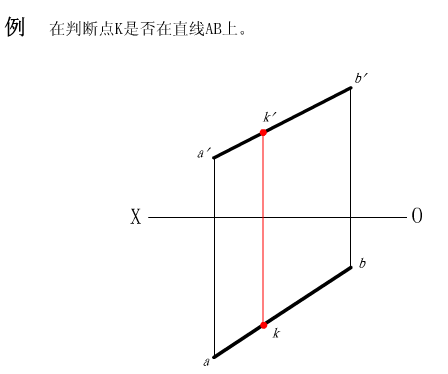
(1)点在直线上,则点的投影必然落在直线的同面投影上。
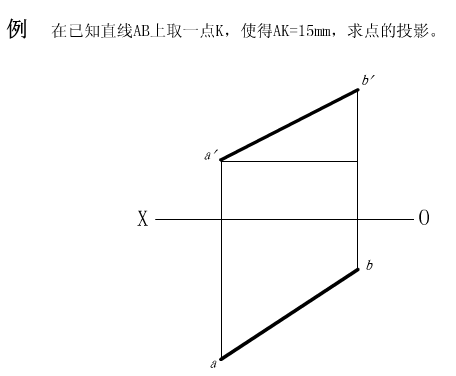
(2)点在直线上,则点分割直线之比在其投影图上保持不变。

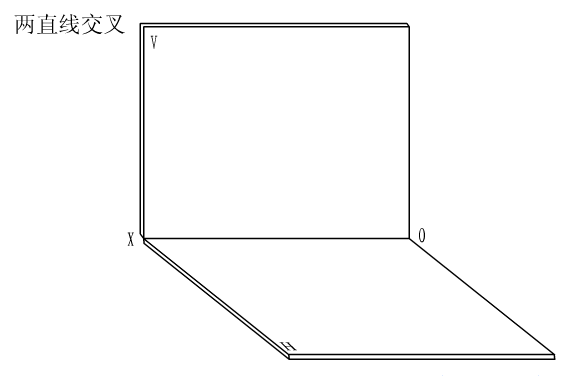
2.4.4 两直线的相对位置
两直线的相对位置有三种情况:平行、相交、交叉(异面)。
1.两直线平行
如果两直线在空间中平行,则它们的各同面投影一定相互平行。反之,如果两直线的各同面投影相互平行,那它们在空间一定平行。
两直线平行一般判定方法:
如果两直线的任何两对同面投影相互平行,就可以判定它们在空间平行。(排除后述的特殊情况)
特殊情况
如果两直线的两对同面投影相互平行但两直线平行于第三投影面,就必须查看它们在所平行的投影面上的投影是否平行。


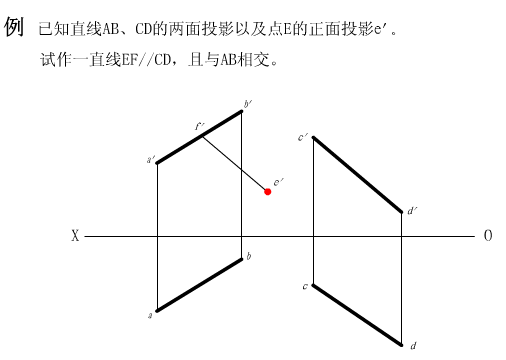
2.两直线相交
如果两直线相交,则它们的各同面投影一定相交,且两直线的各同面投影的交点即为两直线交点的投影。反之,如果两直线的各同面投影相交,且各投影的交点符合投影规律,则此两直线在空间中必定相交。
两直线相交判定方法:
一般情况下,只要有两组同面投影相交且交点符合点的投影规律,则可以判定两直线在空间相交。
特殊情况:两直线其中之一为某投影面平行线时,要根据该投影面上的投影交点来判定。