无标题文档

4.2 两回转体相交

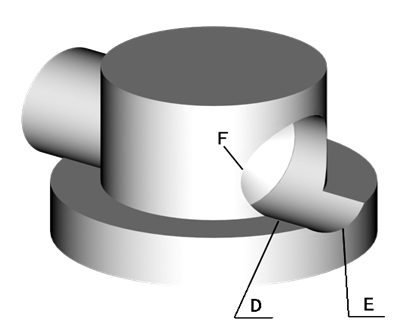
例 4-12 求圆柱与半圆球的相贯线。

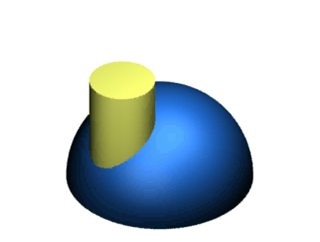
立体相贯的分析和解题方法

1．分析两个相贯的立体分别是下面哪种基本几何体：

四棱柱、六棱柱、圆柱、圆锥（台）、圆球等。

确定两基本几何体与投影面的相对位置及其轴线的相对位置。

2. 想象：两个基本几何体的哪些表面之间相交。

3. 分别求基本几何体表面之间的交线，确定交线的范围，判别投影可见性。针对不同的回转体，采用相应的方法求交线。

4. 补（删）基本几何体的投影。

5. 检查并加深。

4.2.3 相贯线的特殊情况

1．相贯线为平面曲线

（1）两个同轴回转体相贯时，它们的相贯线一定是与轴线垂直的圆。当回转体轴线平行于投影面时，此圆在该投影面上的投影为垂直于轴线的直线。

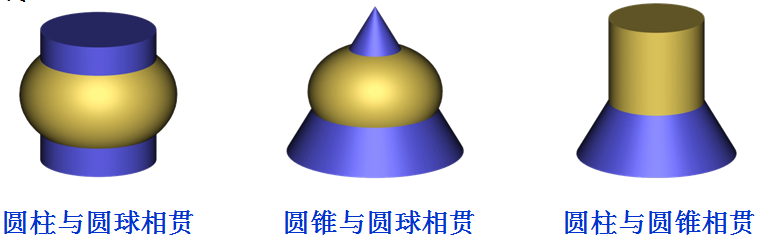
（2）当两个二次曲面公切于一球面时，相贯线是平面曲线椭圆。椭圆所在的平面垂直于两条轴线所决定的平面。

两回转体内切于同一球面

2．相贯线为直线

两圆柱体的轴线平行时，相贯线为直线。

4.2.4 影响相贯线形状的各种因素

影响相贯线形状的因素包括两回转体的形状、大小及其相互位置

两回转体形状、相对位置不变，大小尺寸变化对相贯线的影响。

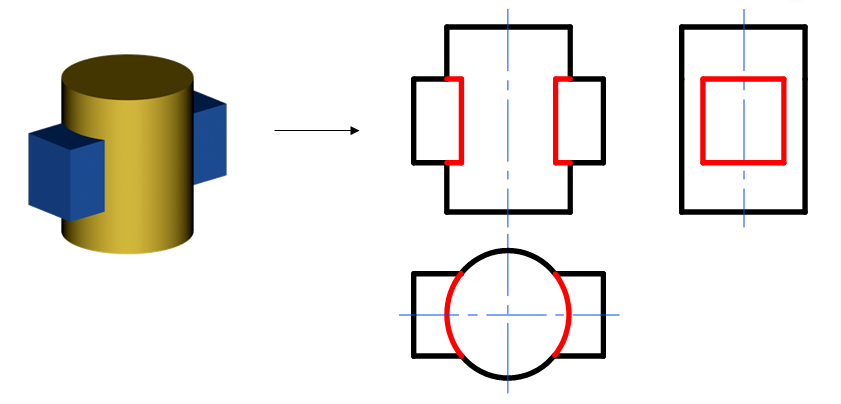
例 4-13 试分析图4-27所示四棱柱和圆柱相交。

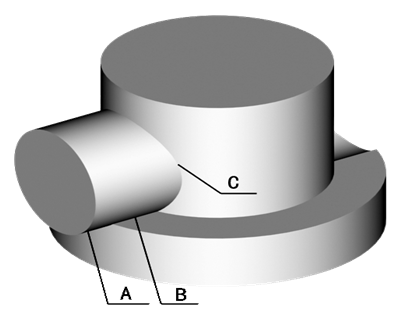
例 4-14 分析图4-26所示组合体的形状及相贯线的投影。